Fun with Microsoft Azure Machine Learning #AzureML – Szenario: Wettervorhersage
Im Dezember habe ich auf dem sepagoForum in Köln einen eher unterhaltsamen Vortrag zu Azure Machine Learning gehalten: „Fun with Azure Machine Learning“. Neben einer kurzen Einführung in neuronale Netze und AzureML habe ich verschiedene Szenarien vorgestellt. In den Szenarien habe ich gezeigt, ob neuronale Netze bestimmte Aufgaben lösen können oder eben nicht. Eines dieser Szenarien stelle ich hier vor.
Szenario: Wettervorhersage/Temperatur des Folgetages
Neuronale Netze sind in der Lage, Vorhersagen aufgrund des Erlernten zu treffen. Ob das auch für die morgige Temperatur gilt, zeigt dieses Experiment. Ziel ist es, dass das Experiment die Durchschnittstemperatur für morgen vorhersagt. Als Eingangsparameter bekommt das Experiment die Durchschnittstemperatur von heute und die der vergangenen 59 Tage.
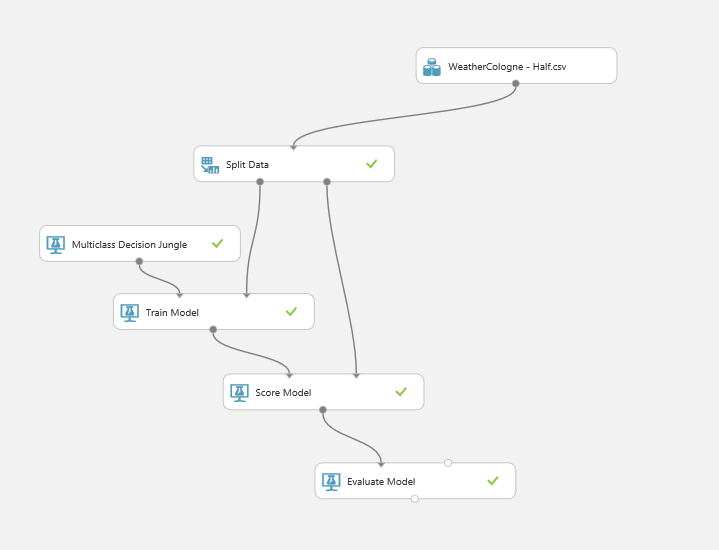
Das Experiment ist in Azure Machine Learning Studio simpel aufgebaut:
Datenquelle und Modellierung
Damit das Experiment lernen kann, benötigt es eine möglichst große Menge an Daten – also Durchschnittstemperaturen in einem zeitlichen Verlauf. Für Köln habe ich auf der Webseite http://www.koelnwetter.de/home/archiv/jahre.html von Klaus G. Rode diese Daten und mehr gefunden. Ab dem 1.1.2007 ist für jeden Tag die Durchschnittstemperatur erfasst. Zur Vereinfachung des Experiments habe ich die Temperaturen gerundet.
Damit stehen über 3000 Datensätze für das Training zur Verfügung. Der erste Datensatz ist am 2.3.2007 komplett. Am 2.3.2007 war die Durchschnittstemperatur 6°C. Am Tag zuvor 10°C und 60 Tage vorher (am 1.1.2007) 7°C. Die ersten Datensätze sehen wie folgt aus:
Entsprechend als CSV zum Import in AzureML:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
t,"t-1","t-2","t-3","t-4","t-5","t-6","t-7","t-8","t-9","t-10","t-11","t-12","t-13","t-14","t-15","t-16","t-17","t-18","t-19","t-20","t-21","t-22","t-23","t-24","t-25","t-26","t-27","t-28","t-29","t-30","t-31","t-32","t-33","t-34","t-35","t-36","t-37","t-38","t-39","t-40","t-41","t-42","t-43","t-44","t-45","t-46","t-47","t-48","t-49","t-50","t-51","t-52","t-53","t-54","t-55","t-56","t-57","t-58","t-59","t-60"6,10,10,7,8,9,10,10,8,9,8,6,4,7,7,6,7,8,9,9,6,4,2,1,3,3,5,6,9,9,8,8,8,6,4,-2,-2,-2,-2,1,7,12,11,13,11,8,3,6,12,11,13,13,18,18,9,10,13,18,19,15,77,6,10,10,7,8,9,10,10,8,9,8,6,4,7,7,6,7,8,9,9,6,4,2,1,3,3,5,6,9,9,8,8,8,6,4,-2,-2,-2,-2,1,7,12,11,13,11,8,3,6,12,11,13,13,18,18,9,10,13,18,19,1510,7,6,10,10,7,8,9,10,10,8,9,8,6,4,7,7,6,7,8,9,9,6,4,2,1,3,3,5,6,9,9,8,8,8,6,4,-2,-2,-2,-2,1,7,12,11,13,11,8,3,6,12,11,13,13,18,18,9,10,13,18,199,10,7,6,10,10,7,8,9,10,10,8,9,8,6,4,7,7,6,7,8,9,9,6,4,2,1,3,3,5,6,9,9,8,8,8,6,4,-2,-2,-2,-2,1,7,12,11,13,11,8,3,6,12,11,13,13,18,18,9,10,13,1810,9,10,7,6,10,10,7,8,9,10,10,8,9,8,6,4,7,7,6,7,8,9,9,6,4,2,1,3,3,5,6,9,9,8,8,8,6,4,-2,-2,-2,-2,1,7,12,11,13,11,8,3,6,12,11,13,13,18,18,9,10,138,10,9,10,7,6,10,10,7,8,9,10,10,8,9,8,6,4,7,7,6,7,8,9,9,6,4,2,1,3,3,5,6,9,9,8,8,8,6,4,-2,-2,-2,-2,1,7,12,11,13,11,8,3,6,12,11,13,13,18,18,9,108,8,10,9,10,7,6,10,10,7,8,9,10,10,8,9,8,6,4,7,7,6,7,8,9,9,6,4,2,1,3,3,5,6,9,9,8,8,8,6,4,-2,-2,-2,-2,1,7,12,11,13,11,8,3,6,12,11,13,13,18,18,9… |
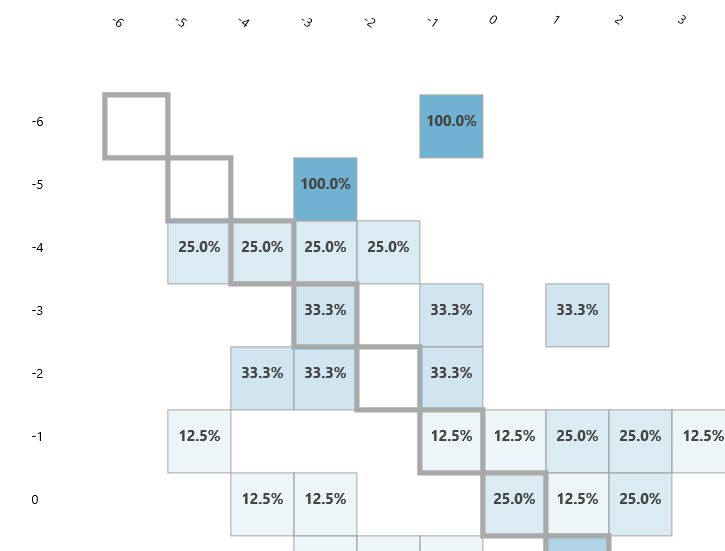
Confusion Matrix
Die Confusion Matrix sieht recht vielversprechend aus. Logisch perfekt wären die Vorhersagen, wenn in der Diagonalen immer 100% stehen würde. Da sich die Wahrscheinlichkeiten jedoch in der Nähe der Diagonalen befinden, erreiche ich anscheinend eine ungefähre Vorhersagbarkeit.
Ergebnisse
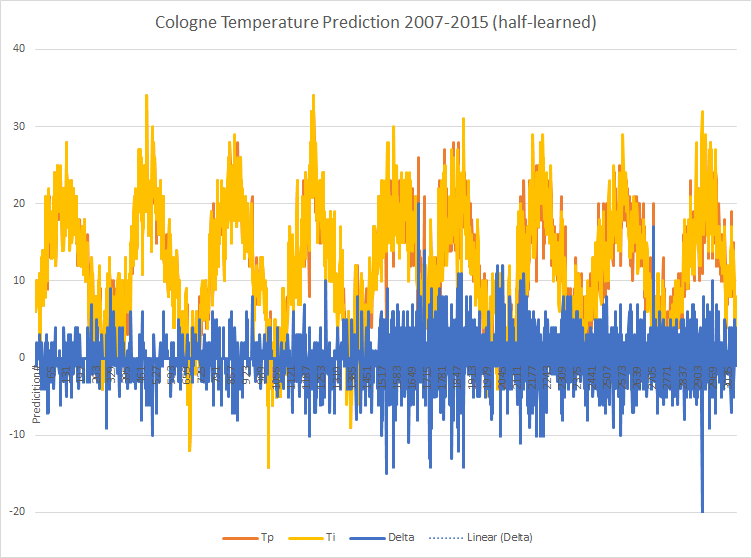
Ich habe das angelernte Modell genutzt, um die Temperaturen der letzten 8 Jahre vorherzusagen (immer auf Basis der Temperatur der vorhergehenden 60 Tage). Da die gemessenen Temperaturen (Ti) bekannt sind, habe ich das Delta zu den vorhergesagten (Tp) ermittelt. P ist die Wahrscheinlichkeit für die einzelne Vorhersage.
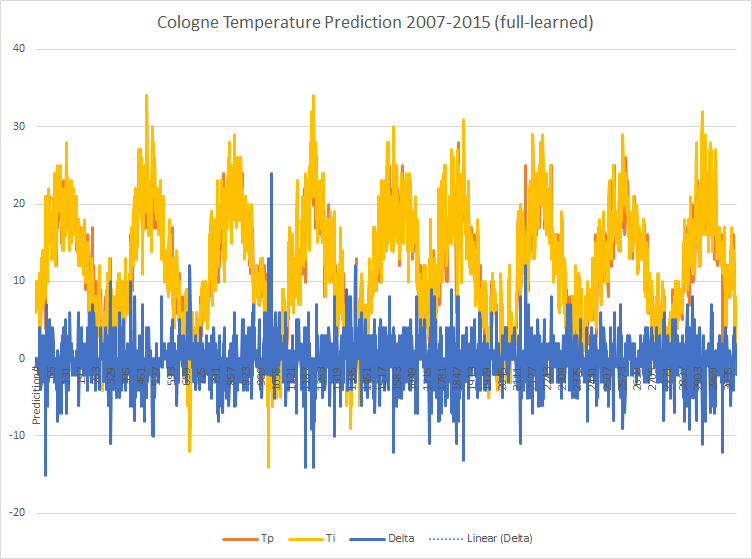
Zu erkennen ist, dass die ersten Vorhersagen kaum von den Messwerten abweichen. Über den gesamten Zeitraum ergibt sich folgendes Bild:
Hineingezoomt zeigt sich ein klareres Bild. Hier die Visualisierung der Datensätze 2000 bis 2138 (ca. im Jahr 2013):
Vorhersage und Messwerte scheinen in vielen Fällen übereinzustimmen bzw. nahe beieinander zu liegen. Nur 6-mal lagen Mess- und Vorhersagewert 5°C auseinander.
Gegenprobe
Aber kann es sein, dass sich die Durchschnittstemperatur so einfach vorhersagen lässt? Die Logik sagt hier eindeutig „Nein“. Das Experiment berücksichtigt weder Wind, Hochs, Tiefs, globale Wetterlage etc.
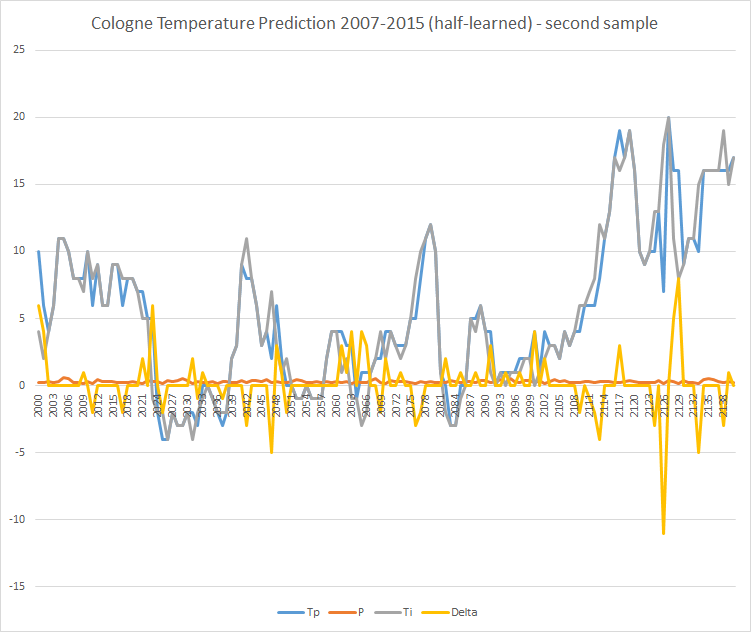
Ich habe das Experiment wiederholt und es mit der Hälfte der Daten lernen lassen (2007 bis 2012) und wieder den Zeitraum von über 8 Jahren vorhersagen lassen und erhalte folgende Ergebnisse:
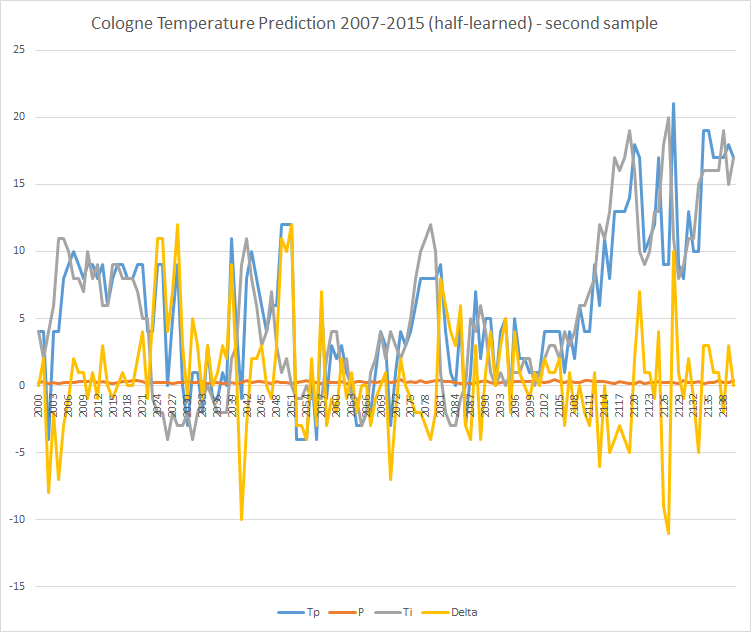
Zu sehen ist, dass in der zweiten Hälfte die Vorhersagen ungenauer werden. Und tatsächlich: In einem Ausschnitt der zweiten Hälfte ist es ungenauer als im „vollständig angelernten“ Modell:
Im selben Zeitraum wie oben kommt es hier zu 26 Abweichungen größer 5°C.
Fazit
Was bedeutet das? Es bedeutet, dass ich das Modell im ersten Fall mit den vollständigen Daten „überlernt“ habe. Das Experiment hat auswendig gelernt und konnte im Rahmen der Testdaten recht „gute“ Voraussagen treffen. Die Voraussagen verlieren in der Zukunft jedoch deutlich an Qualität.
Es ist so, wie es ist. Das Experiment eignet sich nicht für genaue Vorhersagen der morgigen Temperatur. Die Ergebnisse sind eher vergleichbar mit den sogenannten „Bauernregeln“.
Wichtiger sind die Erkenntnisse zum Umgang mit Eingangsdaten, deren Modellierung und vor allem zu Interpretation und Hinterfragen der Ergebnisse.